--Bubble Sort Visualiser--
What Makes A Good Sorting Algorithm?
As with all algorithms, time complexity is a meaningful consideration.
The rate at which computation time grows with respect to input size can be the difference between a program executing in milliseconds and the very same calculation taking days upon days to complete.
In sorting algorithms, the time complexity is typically either O(n^2) or O(nlogn) and the difference between the two is indeed rather notable.
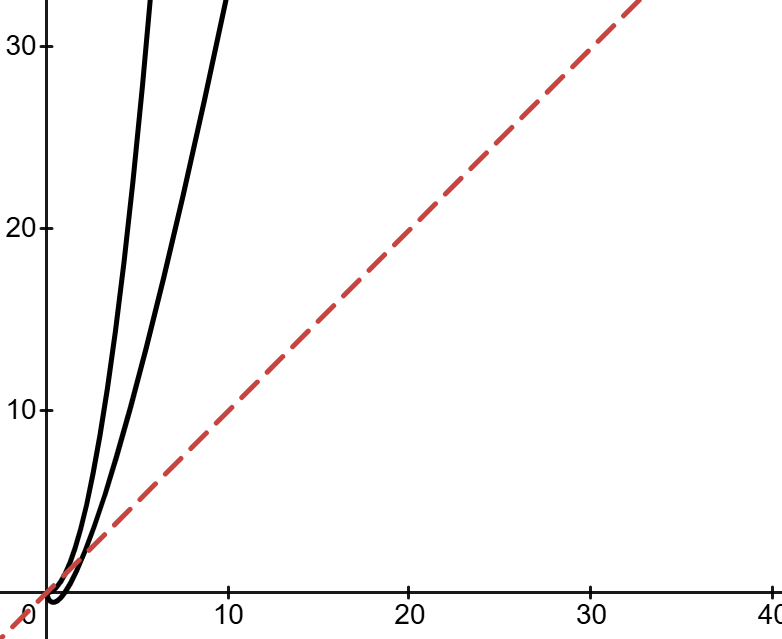
While often mundane, methods of sorting are often peoples first introduction to algorithms through the critical lens of optimisation and feasibility.
As shown in the above graph, O(nlogn) is favourable compared to O(n^2), however neither come close to linear time.
Efficient algorithms have polynomial time complexity (O(n^k)) whereas ones considered impractical and 'brute force' have non-polynomial time complexities (eg O(n!) or O(2^n)).
This means that problems such as seeing if a graph can be coloured with k colours is verifiable but not easily found.
Moreover, questions such as the chromatic number χ of a graph are hard to substantiate.